Furniture Production Line Layout Design

ABSTRACT

This paper experiments application of different heuristic approaches to a real facility layout problem at a furniture manufacturing company. All the models are compared using AHP, where a number of parameters of interest are employed. The experiment shows that formal layout modelling approaches can be effectively used real problems faced in industry, leading to significant improvements.

1. INTRODUCTION

The furniture industry is experiencing a very competitive era like many others, thus striving hard to find methods to reduce manufacturing costs, improve quality etc. As part of a productivity improvement program in a manufacturing company herein called (The Company = TC) we conducted a project to optimize the layout design of the production line at the shop floor of this company aiming at overcoming the current problems attributed to the inefficient layout. It was decided to apply a number of layout modelling techniques to generate a near optimal layout based on formal methods that are rarely used in practice. The modelling techniques used are Graph Theory, Bloc Plan, CRAFT, Optimum Sequence and Genetic Algorithm. These layouts were then evaluated and compared using three criteria namely Total Area, Flow * Dist and the Adjacency Percentage. Total Area refers to the area occupied by the production line for each model developed. Flow * Dist calculates the sum of products of the flow and the distance between every two facilities. Adjacency Percentage calculates the percentage of the facilities that meet the requirement of being adjacent.

Selection of the best layout was also done formally usingmulti-criteriadecision making approach AHP (Satty, 1980) using Expert Choice software. The best layout was compared with the existing layout to demonstrate improvements gained by formal approaches to layout design.

The definition of a plant layout problem is to find the best arrangement of physical facilities to provide an efficient operation (Hassan and Hogg, 1991). The layout affects the cost of material handling, lead time and throughput. It hence affects the overall productivity and efficiency of the plant. According to Tompkins and White (1984) the design of facilities has been around throughout recorded history and indeed town facilities that were designed and built are described in the ancient

* Corresponding Author

history of Greece and the Roman Empire. Among the first who studied this problem are Armour and Buffa et al. (1964). Little seems to have been published in the 1950’s. Francis and White (1974) were the first who collected and updated the early research on this area. Later research has been updated by two studies the first by Domschke and Drexl (1985) and the other by Francis et al. (1992). Hassan and Hogg (1991) reported an extensive study on the type of data required in the machine layout problem. The machine layout data is considered in a hierarchy; depending on how detailed the layout is designed. When the layout required is only to find the relative arrangement of machines, data representing machine number and their flow relationships are sufficient. However, if a detailed layout is needed, more data is required. In finding data some difficulties may arise especially in new manufacturing facilities where the data is not yet available. When the layout is developed for modern and automated facilities, the required data cannot be obtained from historical data or from similar facilities since they may not exist. Mathematical modelling has been suggested as a way to get an optimal solution for the facility layout problem. Since the first mathematical model developed by Koopmans and Beckmann (1957) as a quadratic assignment problem, interest in the area has attracted considerable growth. This opened up a new and interesting field for the researcher. In searching for a solution to the facility layout problem, researchers launched themselves into developing mathematical models. Houshyar and White (1993) looked at layout problem as aninteger-programmingmodel while Rosenblatt (1986) formulated the layout problem as a dynamic programming model. Palekar et al. (1992) deal with uncertainty and Shang (1993) uses amulti-criteriaapproach. On the other hand, Leung (1992) presented a graph theory formulation.

Green andAl-Hakim(1985) used a GA to find the part family as well as the layout between cells. In his formulation, he limited the arrangement of cell as either linear single row or linear double row. The developed algorithm is more towards the cells system layout, or the layout of production floor, rather than the cell layout, or the machine layout. The actual layout of machines within cells was not considered. Banerjee and Zhou (1995) formulated the facilities design optimization problem for asingle-looplayout using genetic algorithms. The developed algorithm is for the cell systems layout and hence does not consider the layout of machines within cell. Fu and Kaku (1997) presented a plant layout problem formulation for a job shop manufacturing system where the objective is to minimize the average Work in Process. They modeled the plant as an open queuing network under a set of assumptions. The problem reduces to a Queuing Assignment Problem (QAP). Simulation was used to minimize the average Material Handling costs and minimizing the Average Work in Process.

2. MODELING APPROACHES

Models are categorised depending on their nature, assumptions and objectives. The first generic Systematic Layout Planning approach, developed by Muthor (1955), is still a useful scheme specially if supported by other approaches and assisted by computer. Construction approaches, Hassan and Hogg (1991) for example, build a layout from scratch while Improvement Methods, Bozer, Meller and Erlebacher (1994) for example, attempt to modify an existing layout for better results. Optimising methods and also heuristics for layout by is well documented by Heragu (2007).De-Alvarengaand Gomes (2000) discuss ameta-heuristicapproach as a way to overcome the NP- hard nature of optimal models.

The various modelling techniques used in this work are Graph Theory, CRAFT, Optimum Sequence, BLOCPLAN and Genetic Algorithm. Explained below are parameters that are required by each algorithm in order to model the same.

Graph Theory

Graph theory (Foulds and Robinson, 1976; Giffin et al., 1984; Kim and Kim, 1985; and Leung, 1992)applies anedge–weightmaximal planar graph in which the vertices (V) represents the facilities and the edges (E) represent adjacencies and Kn denotes the complete graph of n Vertices. Given a weighted graph G, the facility layout problem is to find a maximum weighted spanningsub-graphG’ of G that is planar.

This paper uses 2 different kinds of approaches to model the case study. The first approach is theDelta-hedronmethod by Foulds and Robinson (1976). The method involves simple insertion with an initial K4, and vertices are then inserted one by one according to a benefit criterion. The second approach used is the wheel expansion algorithm (Green andAl-Hakim,1985). Here the initial K4 is obtained by selecting an edge having the highest weight and then applying two successive vertex insertion according to the benefit criteria. The algorithm then proceeds with an insertion process, called the wheel expansion procedure. A wheel on n vertices is defined as a cycle on(n-1)vertices (termed the rim), such that each vertex is adjacent to one additional vertex (termed the hub). Let W be a wheel having the hub x. Select two vertices k and l, which are the rims of this cycle. A vertexy from the set of unused vertices is then inserted to this wheel in the current partialsub-graphsuch that y is a hub of the new wheel W′ containing k, l and x as its rims, and all rims in W are now adjacent to vertex x or vertex y. By inserting each unused vertex successively in the above fashion, the final maximal planar sub graph is obtained.

Using CRAFT

CRAFT (Computerized Relative Allocation of Facilities Technique) uses a pair wise exchange to develop a layout (Buffa et al., 1964; Hicks and Lowan, 1976). CRAFT does not examine all possible pair wise exchange before generating an improved layout. The input data includes dimensions of the building and facilities, flow of material or frequency of trips between facility pairs and cost per unit load per unit distance. The product of the flow (f) and distance (d) provides the cost of moving materials between 2 facilities. The cost reduction is then calculated based on the pre and post exchange material handling cost contribution.

Optimum Sequence

The method of solution starts with an arbitrary sequential layout and tries to improve it by switching two departments in the sequence (Heragu, 1997). At each step, the method computes the flow*distance changes for all possible switches of two departments and chooses the most effective pair. The two departments are switched and the method repeats. The process stops when no switch results in a reduced cost. The input required to generate a layout using Optimum Sequence are mainly dimensions of the building and facilities, the flow of material or frequency of trips between facility pairs and cost per unit load per unit distance.

Using BLOCPLAN

BLOCPLAN is an interactive program used to develop and improve both single and multi storey layout (Green and Al-Hakim,1985). It is a simple program which generates good initial layouts due to its flexibility based on several imbedded options. It uses both quantitative and qualitative data to

generate several block layouts and their measure of fitness. The user can choose the relative solutions based on circumstances.

Genetic Algorithm

There are numerous ways of formulating facilities Layout problems through genetic algorithms(GA).Banerjee, Zhou, and Montreuil(1997) applied GA to cell layout.. Slicing tree structure was first suggested by Otten (1982) as a way to represent a class of layouts. The approach was later used by many authors including Tam and Chan (1995) who used it to solve the unequal area layout problem with geometric constraints. The GA algorithm used in this work was developed by Shayan and Chittilappilli (2004) based on slicing tree structures (STC). It codes a tree structured candidate layout into a special structure of 2 dimensional chromosomes which shows the relative location of each facility in a slicing tree. Special schemes are available to manipulate the chromosome in GA operations (Tam and Li, 1991). A new “cloning” operation was also introduced in Shayan andAl-Hakim(1999). The chosen solution through GA is then converted to a slicing layout. It starts with one initial block that contains all the facilities. As the layout constructing algorithm progresses, new partitions are made and facilities are assigned between newly generated blocks, until there is only one facility in each block. Meanwhile the coordinates of each facility is also calculated. Rectilinear distance between centroids of facilities is used to evaluate the fitness of the respective chromosome. When the GA terminates, a drawing procedure takes over to print the layout using the stored values of the coordinates. The objective function has a penalty term to avoid narrow slices.

3. EXPERIMENTATION VIA A CASE STUDY

To test the performance of the methods described before, they were all applied to a real case scenario in furniture manufacturing. The Company manufactures 9 different styles of Chairs, 2- Seaters and3-Seatersrespectively. Production of all the styles follows the same set of operations but involve different raw materials. 5 parts namely Seat cushions, Back cushions, Arms Seats and Backs are produced internally in batches of varied sizes, in scattered areas (departments). Movement of parts generates problems such as work in progress, missing parts, shortages, congestion and wrong placement.

Each product goes through 11 operations which begin at Facility 1 – Cutting Area and end at Facility 11- Bolt up Area. Each of the final assembly can be broken down into subassemblies named the same. These subassemblies meet up at the Bolt-UpFacility for final assembly. Each of the subassemblies begin their operations independently and all go through a fixed set of operations which is shown in the form of an assembly chart in Fig 1. The facilities of the current layout are not placed according to the sequence of operations.

Due to this there is no sequential flow of materials, giving rise to work in progress. The interaction between facilities can be determined using subjective as well as objective measures. The main input required for flow charts is the demand, the quantity of materials produced and the amount of material that flows between each machine. The flow of material is calculated based on amount of flow of material traveling per 10 months * Unit of measure which is shown in Figure 2. Figure 3 shows the area of each of the department used in the case study. Figure 4 shows the current layout of the Case Study.

Figure 1 Assembly chart for the case study

Figure 2 Flow of material for the case study.

Figure 3 Number corresponding to the department

Figure 4 Current layout of the furniture company and the dimensions of each department used in the modelling of the case study

4. APPLICATION OF THE MODELING APPROACHES

Here the various modelling approaches discussed in section 2 are applied to the case study to generate alternative layouts for comparison.

4.1 Using Graph Theory

Table 1 shows the comparison of the results using two different approaches of Graph Theory namely the Foulds and Robinsons method and the Wheels and Rims method. Table 1 it clearly shows that the Foulds and the Robinsons method is the better of the two results. The results of the Foulds and Robinsons method are explained in detail in Figures5-7.

Table 1: A table showing the comparison of the two different methods of graph theory used.

Figure 5 Adjacency graph of case study results using Foulds and Robinson method.

Figure 6 Improved layout after using graph theory (Foulds and Robinsons method)

1-Cutting,2- Sewing, 3- Fill Calico, 4- Close Up, 5 - Fill cushion insert, 6- Foam Cutting, Foamcutting,7- Frame Assembly, 8- Sticking,9-SpringUp,10-Upholstery,11- Bolt Up.

Figure 7 Flow * Distance evaluation chart for the case study using graph theory (Foulds and Robinsons method)

4.2 Using CRAFT

The input data for CRAFT is entered and the initial cost for the current layout is first calculated. This cost can be reduced using a pair wise comparison as shown in Figures 8,9.

Figure 8 Initial cost for the current layout using CRAFT

Figure 9 Step by step exchange by CRAFT

The results obtained by CRAFT are shown in Table 2. Based on the above calculations a new and improved layout can be drawn which is shown in Figure 10

Table 2: A table showing the results

Figure 10 Improved layout generated by CRAFT

4.3 Optimum Sequence Algorithm

The input data is the same as for CRAFT except that it follows a different set of pair wise comparison. Table 3 shows the results drawn from the improved layout. Figure 11 shows the improved layout using Optimum Sequence.

Table 3 A table showing the results using CRAFT

Figure 11 Improved layout after using optimum sequence

4.4 Using BLOCPLAN

The Flow matrix chart was converted to a REL chart as shown in Figure 12 with the following parameters:

Figure 12 REL Chart for the case study

Table 4 shows the results using different kinds of approach. As seen the BLOCPLAN using an automated search showed better results than using the Construction Algorithm.

Figure 13 Improved layout automated search

Table 4 The measures for BLOCPLAN layouts

4.5 Using Genetic Algorithm

The best solution found by the algorithm is shown in Figure 14. This is then converted to the layout in Figure 15 for common comparisons with other models.

Figure 14 Layout developed by genetic algorithm

Figure 15 Conversion of layout in Fig 14

Table 5 shows the results using Genetic Algorithm.

Table 5 A table showing the results using genetic algorithm

5. COMPARISONS OF EXPERIMENTATION RESULTS BY AHP

Table 6 summarizes the results obtained from all the modelling techniques versus the Current Layout for comparison. Section of the best layout will be done based on three factors namely Total Area (Minimze), Flow * Distance (Maximize) and the Adjacency percentage (Maximize). The main objective is to reduce the WIP and organise a systematic flow of materials. As a result the flow * distance matrix is the most important parameter.

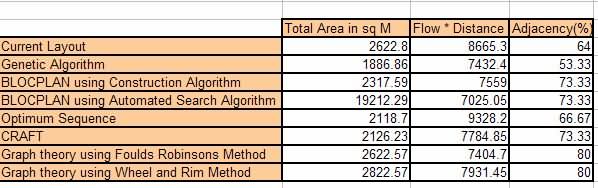
Table 6 Summary of results using all modelling techniques versus the results of the current layout

Table 7 shows the mix ranking of the alternative layouts based on various factors. For example Layout 1 has a poor rank in Area and F*D while is the best in Adjacency. The combination makes it difficult to choose one over the others. We urge to use a formal technique, AHP, implemented by Expert Choice software.

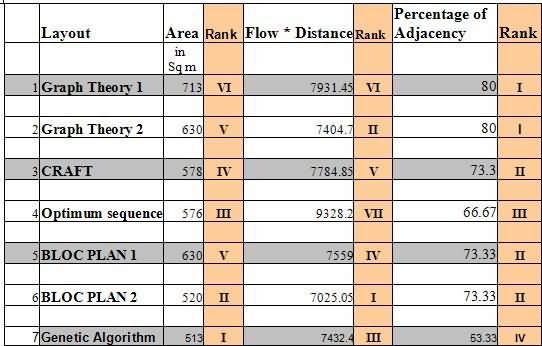
Table 7 Ranking of various alternatives with respect to the objectives

AHPcompares the relative importance of each pair of children with respect to the parent. Once the pair comparisons is completed, the approach synthesis the results using some mathematical models to determine an overall ranking. Figure 16 shows the ranking of the results achieved from all algorithms with respect the goal of best choice solution.

Figure 16 Synthesis with respect to the goal

The best solution is achieved by BLOCPLAN ( Automated Search) followed by Graph Theory using Foulds and Robinsons Method, then Genetic Algorithm. The other solutions are far worse. Note that due to the inherent subjectivities ranking is not an absolute indication of better choice, rather it is a recommendation that the user can entertain to suit the needs.

We propose the layout generated using BLOCPLAN using Automated Search to be the chosen solution. When this was decided a sensitivity analysis was conducted to ensure that the choice is robust. If time allows this should be done for other close alternatives before the choice is made.

6. CONCLUSIONS

The goal in this paper was to use various modelling techniques to select the best layout for a furniture company. The best layout was generated by BLOCPLAN using Automated Search as in Figure 17.

Figure 17 Best layout using modeling approaches

Table 9 shows the improvements of the proposed solution over the current layout. Note that the layout shows the blocks and their relative locations. Practical limitations need to be applied to suit all the needs. Then further details of each block can be planned, if necessary in the same manner.